Add − 2 2 and 4 4 Plug in the slope of the tangent line and the x x and y y values of the point into the point slope formula y−y1 = m(x−x1) y y 1 = m ( x x 1) Simplify Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yinterceptT 5 7 360 70 (1) 54 (2) 75 (3) 68 Q) qjB Using integration, find the area of the region bounded by the parabola y^2 = 4x and the circle 4x^2 4y^2 = 9 asked Mar 17 in Definite Integrals by Takshii (

Write The Definite Integral That Represents The Area Of The Region Enclosed By The Parabola Y 4x X 2 And The X Axis Then Evaluate The Integral Study Com
The region bounded by the parabola y=4x-x^2
The region bounded by the parabola y=4x-x^2-The area bounded by the parabola y^2 = x , straight line y = 4 and y axis is > 12th > Maths > Application of Integrals > Area Under Simple Curves > The area bounded by the parClick here👆to get an answer to your question ️ If the x axis divide the area of the region bounded by the parabolas y = 4x x^2 and y = x^2 x in the ratio of a b then ab is equal to




Graph Of Y 4x 1 Novocom Top
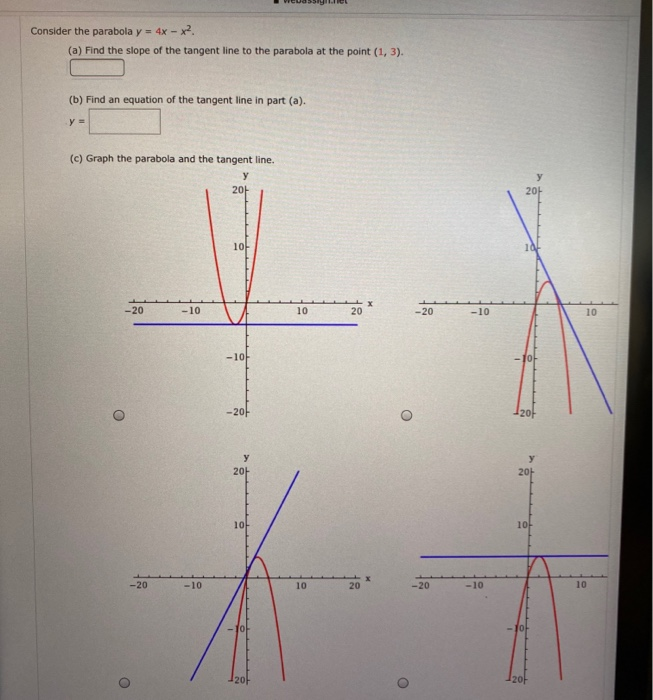
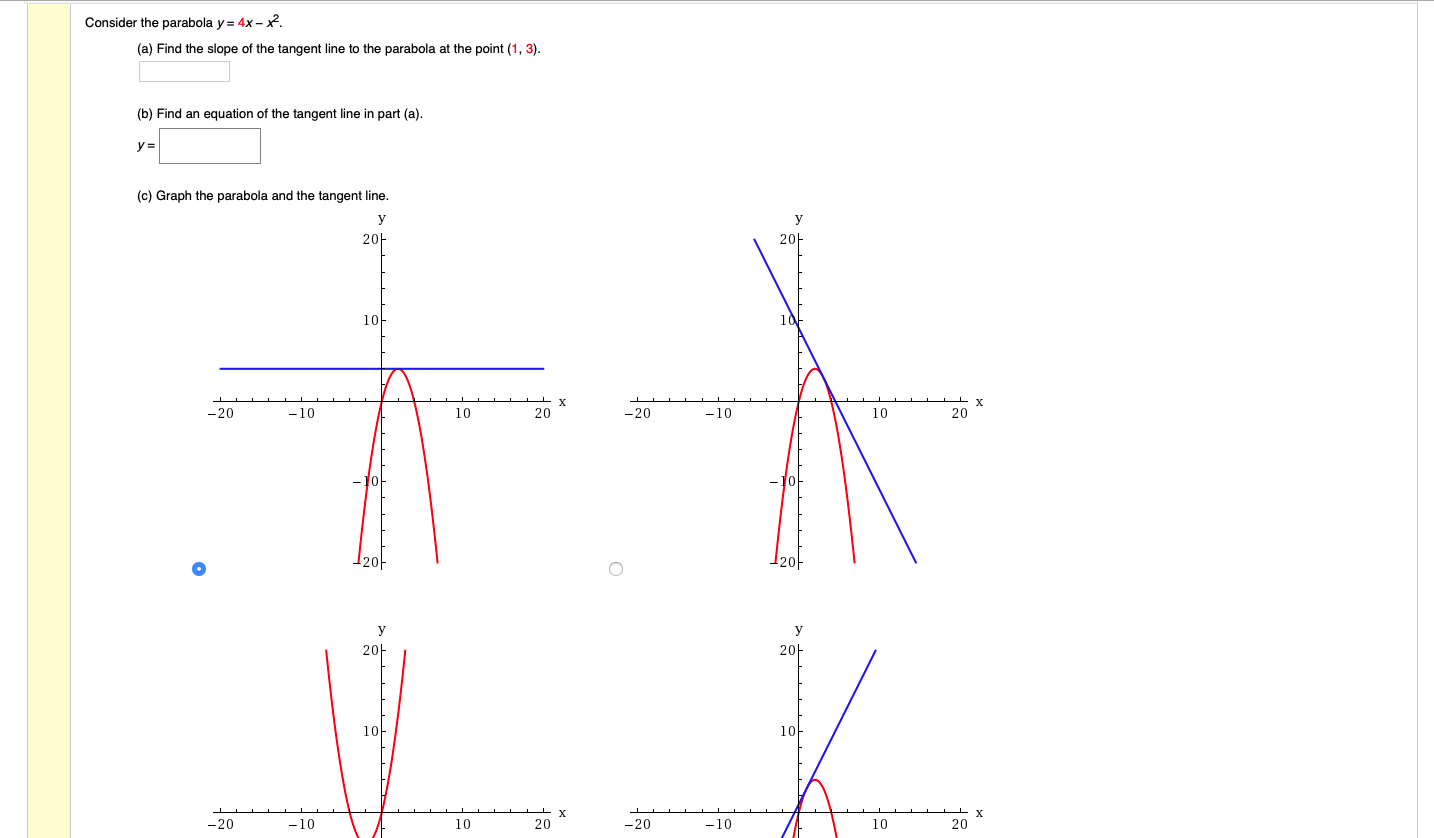
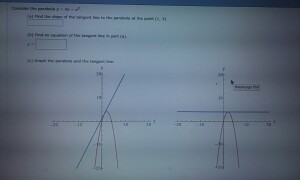
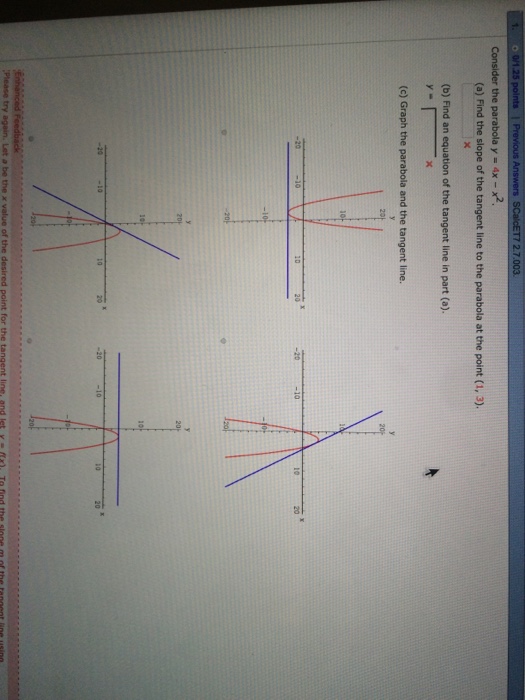
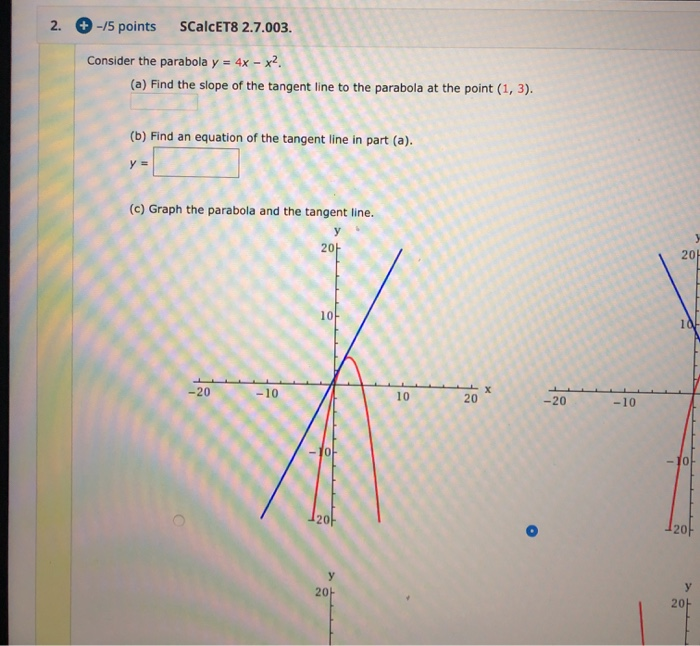
Consider the parabola y = 4x − x2 (a) Find the slope of the tangent line to the parabola at the point (1, 3) (b) Find an equation of the tangent line in part (a) y = (c) Graph the parabola and the tangent line Question Consider the parabola y = 4x − x2 (a) Find the slope of the tangent line to the parabola at the point (1, 3)Answer to The region bounded by the parabola y = 4x x^2 and the x axis is revolved about the x axis Find the volume of the solid WriteThe area bounded by the curve mathy = 4x x^2/math and the line mathy = 3/math is a simple integral mathy = 4x x^2/math is an upsidedown parabola mathy = 3/math is a horizontal line that crosses the parabola to form a Dshape
Find the Area Between the Curves y=x^2 , y=4xx^2 y = x2 y = x 2 , y = 4x − x2 y = 4 x x 2 Solve by substitution to find the intersection between the curves Tap for more steps Substitute x 2 x 2 for y y into y = 4 x − x 2 y = 4 x x 2 then solve for x x Tap for more steps0 votes 1 answer Draw a rough sketch and find the area of the region bounded by the two parabolas y^2 = 4x and x^2 = 4ySee the answer a) Find the slope of the tangent line to the parabola y =4xx 2 at the point (1,3) (i) using definition 1 (ii) using equation 2 b) Find an equation of the tangent line in part (a)
Assume matha>0 /mathbecause the arc length will be same for corresponding negative values of matha/math The formula is simple enough (see Calculus II Arc Length) So is the derivative But life gets positively nasty when we calculate thX = 0 x = 4 are the limits math\displaystyle \int_0^4 \, 4x x^2 \, dx \implies \left 2x^2 \frac{x^3}{3} \right_0^4 \impConsider the parabola y = 4x x^2 (a) Find the slope of the tangent line to the parabola at the point (1, 3) _____ (b) Find an equation of the tangent line in part (a) y = _____ (c) Graph the parabola and the tangent line



How To Find The Volume Of The Solid Generated By Revolving The Region Bounded By Math Y 4x X 2 Math Math Y X Math About The Y Axis Quora



Parabolas
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators14 A The parabola Y =3x2 — (1) 55 (2) 24x55 can be written in the form (3) (4) 24 graph q check êQvl = 5 15 The height of an object in meters above the ground is given by wvhere t the time, in seconds For which of the following intervals of t is the object above a height of 350 meters?Se muestra la ecuacion de una parabola en su forma reducida (x2)^2=8(y4) Se determina vertice, foco y recta directriz de la parabola Se realiza un boceto
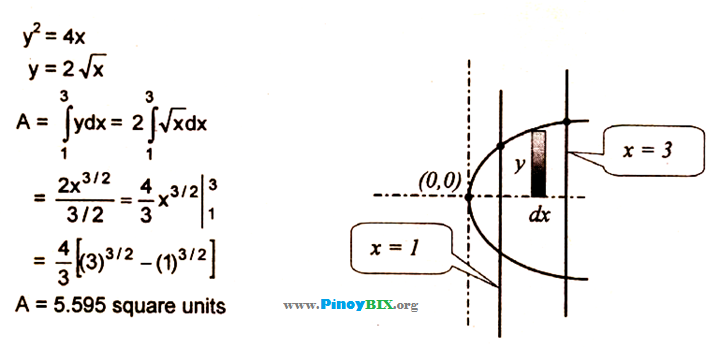



Solution Find The Area In The First Quadrant Bounded By The Parabola Y 2 4x



What Is The Area Bounded By Parabola Y 4x X2 And X Axis Quora
What is the area lying above the xaxis and under the parabola y=4xx^2?The area Targeted above the curveFind the gradient of the tangent to the parabola y=4xx^2 at (0,0) hence calculate the size of the angle between the line y=x and this tangent (as i cant show you the diagram all that it shows is the line going through (0,0) and having one point of Calculus Sketch a graph of the parabola



Find The Area Enclosed By The Parabolas Y 4x X 2 And Y X 2 X Sarthaks Econnect Largest Online Education Community
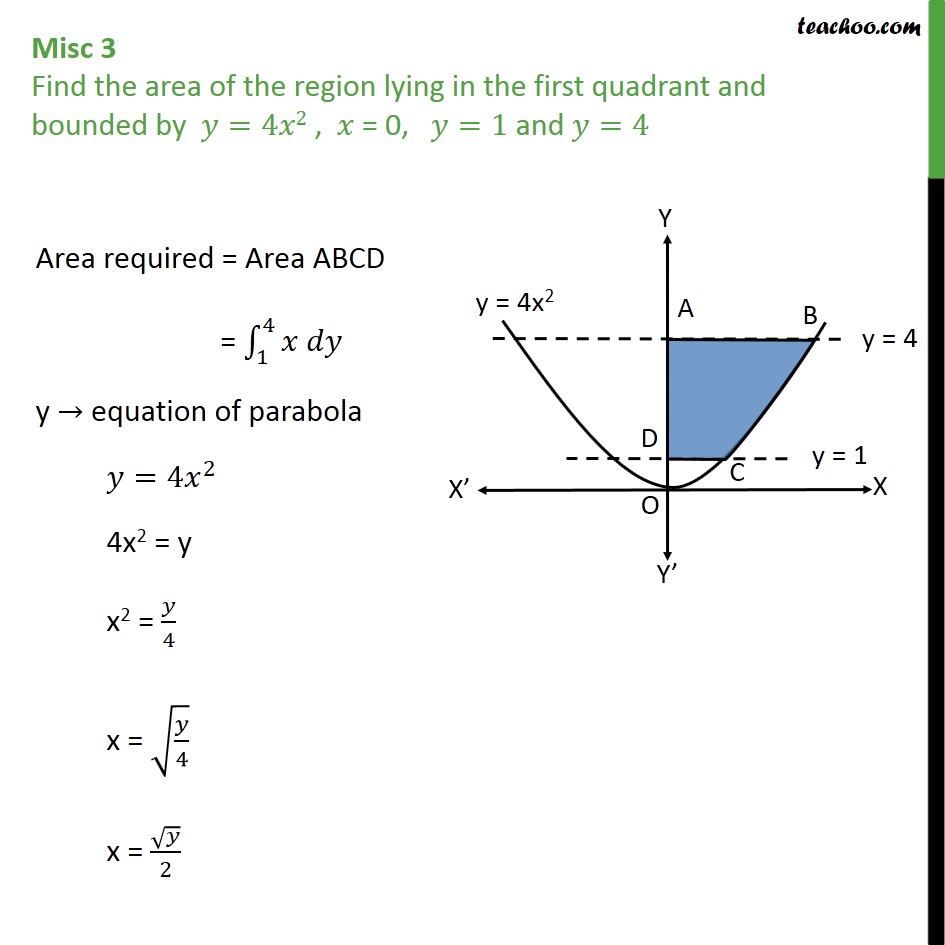



Misc 3 Find Area Bounded By Y 4x2 X 0 Y 1 Y 4
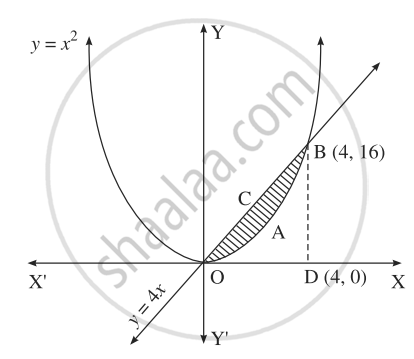
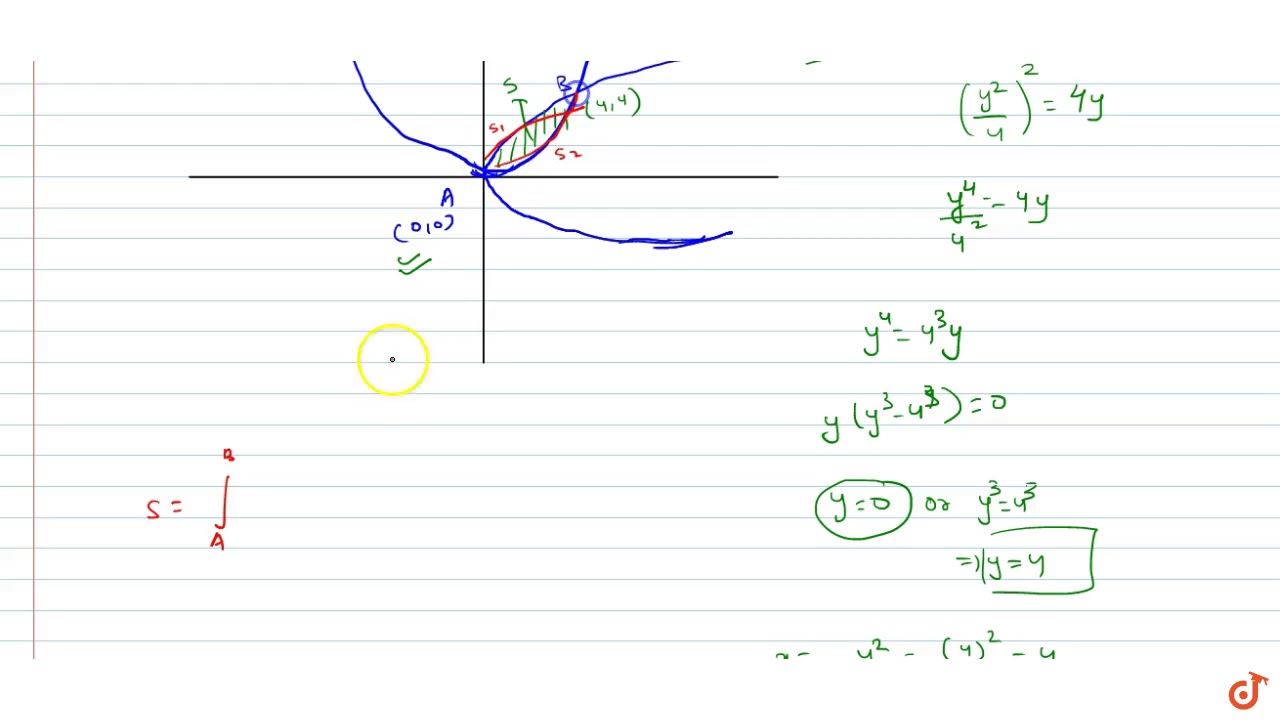
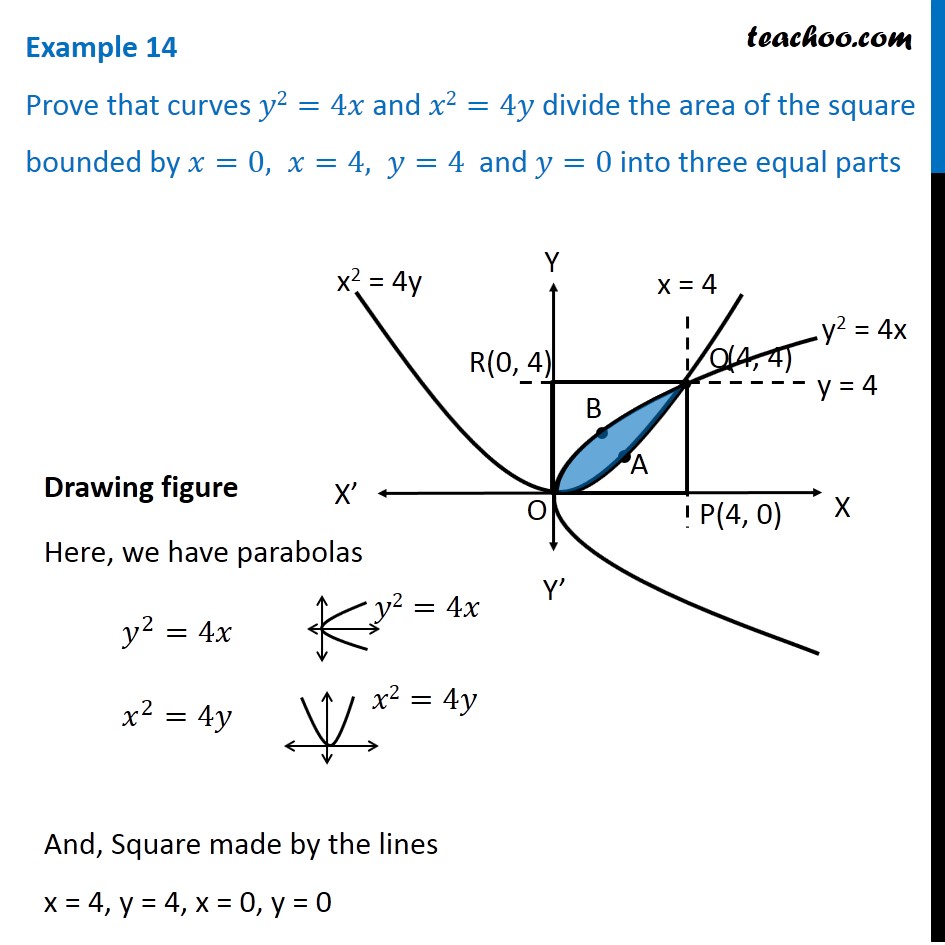
Consider the parabola y = 4x x^2 (a) Find the slope of the tangent line to the parabola at the point (1,3) (b) Find the equation of the tangent line in part (a) y = (c) Graph the parabolaStack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange The parabolas y 2 = 4x and x 2 = 4y divide the square region bounded by the lines x = 4, y = 4 and the coordinate axes If S 1, S 2 and S 3 are respectively the areas of these parts numbered from top to bottom, then S 1 S 2 S 3 is equal to (a) 1



What Is The Area Bounded By The Curve Y 4x X And The Lines X 0 And Y 4 Quora




Example 14 Prove That Y2 4x X2 4y Divide Area Of Square
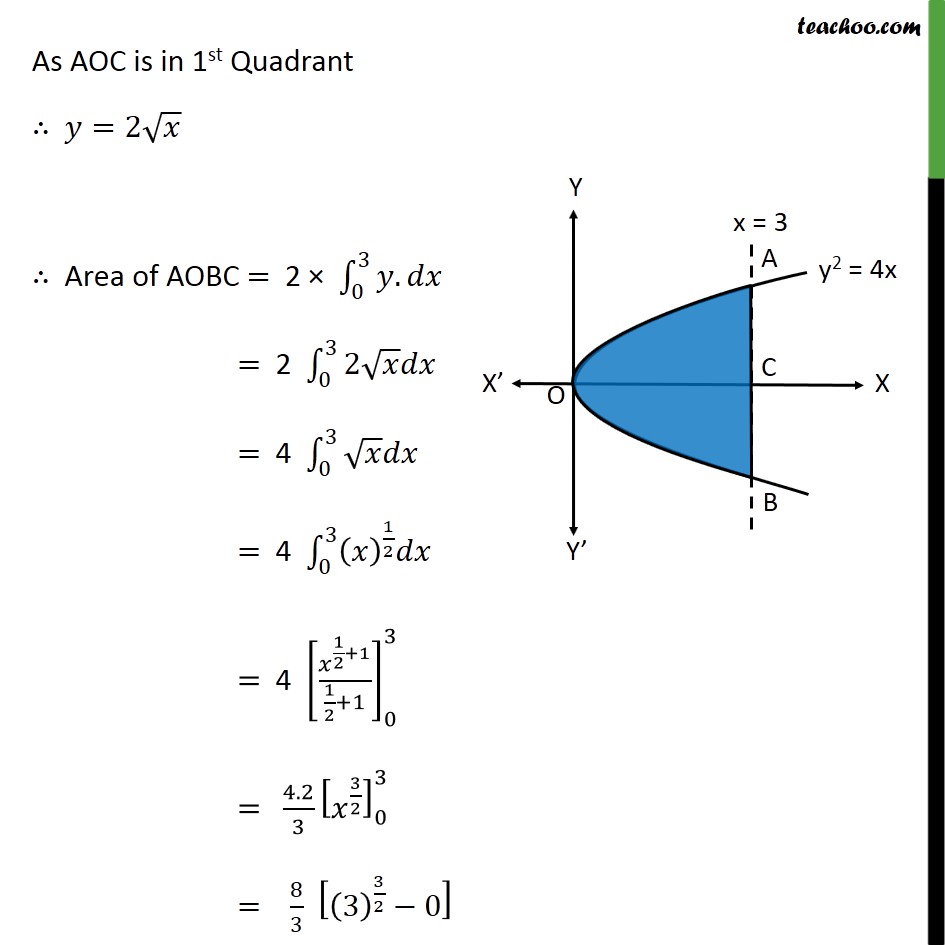
Solution There Are Two Tangent Line To The Curve Y 4x X 2 That Pass Through The Point 2 5 Find The Equations Of These Two Lines And Make A Sketch To Verify Your ResultsIn this case, the equation of the parabola comes out to be y 2 = 4px where the directrix is the verical line x=p and the focus is at (p,0) If p > 0, the parabola "opens to the right" and if p 0 the parabola "opens to the left" The equations we have just established are known as the standard equations of a parabolaFind the area of the region bounded by the parabola y^2 = 4x, the xaxis, and the lines x = 1 and x = 4 asked in Definite Integrals by Siwani01 ( 504k points) area of bounded regions
.png)



The Area Bounded By The Curve Y 4x X2 And The X Axis Is A 307sq Units Maths 1745 Meritnation Com
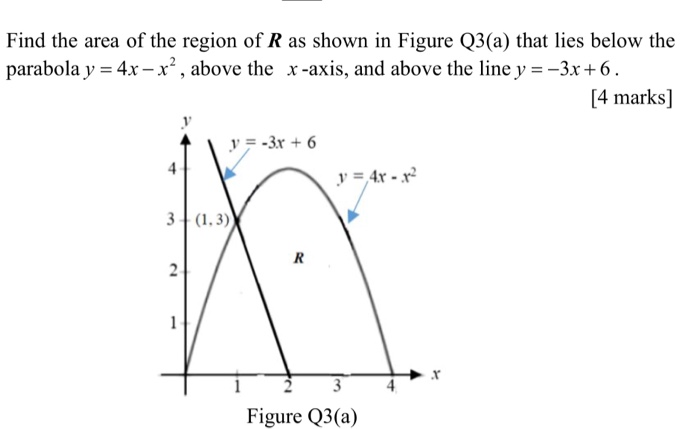



Solved Find The Area Of The Region Of R As Shown In Figur Chegg Com
The area targeted is above the curve, below y =4, and to the right of x = 0 The integral of (4x x^2) gives the area below the curve from x=0 to x =2;Find the area lying above the xaxis and under the parabola y = 4x − x 2 Advertisement Remove all ads Solution Show Solution \\text{ The equation }y = 4x x^2\text{ represents a parabola opening downwards and cutting the }x \text{axis at O(0, 0) and }B(4, 0)\Z u Find the volume generated by revolving the area cut off from the parabola y = 4x — x2 by the x axis about the line y = 6 We divide the area vertically (Fig 4110) The solid generated by revohnng the approximating rectangle about the line y = 6 is a washer whose volume is Ax— qr(6 — Ax The required volume is then Fig 4113 (6)2




2 Find The Area Lying Above The X Axis And Under Gauthmath



Solution How Many Times Does The Parabola Y 4x 2 12x 9 Intersect The X Axis
Graph y=4xx^2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Reorder and The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabola In this video, we are finding the area between parabolas We are setting up a single integral that gives the area of the region bounded by the curves y = x^2This factors to 4x x² = 0 ==> x(4 x) = 0;



How Do You Find The Area Between The Curves Y 4x X 2 And Y X Socratic



Find The Area Of The Region Included Between Y X2 And The Line Y 4x Mathematics And Statistics Shaalaa Com
In what ratio does the xaxis divide the area of the region bounded by the parabolas y = 4x – x^2 asked May 7 in Definite Integrals by Rachi (296k points) area of bounded regions; A parabola's axis of symmetry is a line that runs through its middle and divides it in half For a quadratic of the form #x = ay^2 by c#, the axis is a line that passes through the vertex and is parallel to the #y# axis For our parabola, the axis is the line #y = 2The directrix of a parabola is the vertical line found by subtracting from the xcoordinate of the vertex if the parabola opens left or right Substitute the known values of and into the formula and simplify Use the properties of the parabola to analyze and graph the parabola




Sketch The Region R That Lies Below The Parabola Y 4x X 2 Above The X Axis And Above The Line Y 3x 6 Find The Area Of This Region R Study Com




Content Transformations Of The Parabola
The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabola opens up or down Substitute the known values of and into the formula and simplify Use the properties of the parabola to analyze and graph the parabolaAs A Check On Yourwork, Zoom In Toward The Point (1,3) Until The Parabola And Thetangent Line Are Indistinguishable This problem has been solved!12 bronze badges 2 Add a comment 0 hint The points on the parabola are P = ( x, y) = ( x, 4 x − x 2) for 4 ≥ x ≥ 1 and d y = d y d x d x = ( 4 − 2 x) d x




Solution What Is The Area Bounded By The Curve Y 2 4x And X
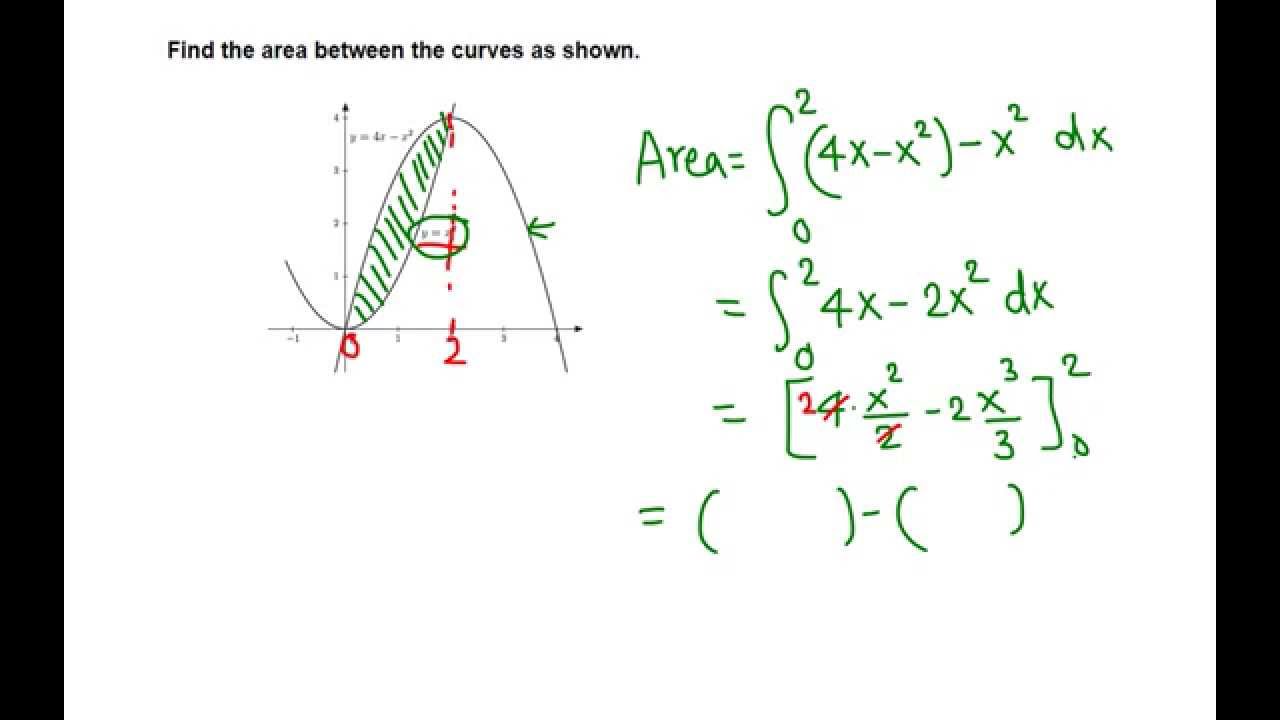



Area Between Y 4x X 2 And Y X 2 Youtube
= = 2x^2 x^3/3 From x = 0 to x = 2 = 8–8/3 =24/3–8/3 = 16/3;The parabola y=4x^2 around y=2 , we drag orginal point from (0,0) to (0,2) →the parabola y=4x^22 around y=0 limited by y=18 and x=0 y=4x^22 by limited y=18 →18=4x^22 → 4x^2=16 →x=2 or x=2 Volume =∫∫∫dxdydz = ∫∫∫dydzdx But dydz=rdrdф ∫∫dydz=A region bounded by the parabola y = 4x − x 2 and the xaxis is revolved about the xaxis A second region bounded by the parabola y = 4 − x 2 and the xaxis is revolved about the xaxis Without integrating, how do the volumes of the two solids compare?



What Is The Volume Of The Region Bounded By Y 4x X 2 And Y X 2 If Rotated About The Line X 4 Quora
/1000px-Parabola_features-58fc9dfd5f9b581d595b886e.png)



How To Find Quadratic Line Of Symmetry
Find the slope of the tangent line to the parabola y=4xx^2 at the point (1,3) 1 See answer itsyeboi2585 is waiting for your help Add your answer and earn points ejelonubenedict ejelonubenedict Y=4x x² dy/dx = 42xGraph a parabola by finding the vertex and using the line of symmetry and the yintercept(a) Find the slope of the tangent line to the parabola y =4xx^2 at the point (1,3) (i) using Definition 1 (ii) using Equation 2 (b) Find an equation of the tangent line in part (a) (c) Graph the parabola and the tangent line As a check on your work, zoom in toward the point (1,3) until the parabola and the tangent line are indistinguishable




Graph Of Y 4x 1 Novocom Top




The Area Bounded By The Curve Y 4x X 2 And X Axis Is A 30 7 Sq Units B 31 7 Sq Units Youtube
Ada 2 metode menghitung volume benda putar dengan menggunakan integral, yaitu 1 Metode cakram berdasarkan rumus Volume = Luas Alas × tinggi Luas Alas selalu berupa lingkaran sehingga Luas Alas = πr2 (r adalah jarijari putaran) digunakan jika batang potongan yang dipilih tegak lurus dengan sumbu putar 2 Metode cincin silinder berdasarkan pengertian bahwa jikaAnswer to Consider the parabola y = 4x x^2 Graph the parabola and the tangent line to the parabola at the point (1, 3) By signing up, you'llThe equation of the parabola is y = 4 – x 2 ∴ x 2 = 4 – y, ie (x – 0) 2 = – (y – 4) It has vertex at P(0, 4) For points of intersection of the parabola with Xaxis, we put y = 0 in its equation ∴ 0 = 4 – x 2 ∴ x 2 = 4 ∴ x = ± 2 ∴ the parabola intersect the Xaxis at




Consider The Parabola Y 4x X 2 Graph The Parabola And The Tangent Line To The Parabola At The Point 1 3 Study Com




Find The Area Bounded By The Parabola Y 2 4x And The Straight Line X Y 3 Youtube
If the parabola \(y = 3x^2 1\) is shifted \(\text{2}\) units to the right, determine the equation of the new parabola Carl's answer A shift to the right means moving in the positive \(x\) direction, therefore \(x\) is replaced with \(x 2\) and the new equation is \(y = 3(x 2)^2 1\)




Determine The Area Of The Region Bounded By The Parabola Y 4x 2 The Tangent Line To This Parabola At 2 16 And The X Axis Study Com



How To Graph A Parabola Y 4x 2 Socratic




Ex 8 2 7 Area Lying Between Y2 4x And Y 2x Is Ex 8 2
.png)



Find The Area Lying Above The X Axis And Under The Parabola Y 4x X2 Maths Meritnation Com



The Region Between Y 4x X 2 And The X Axis Is Rotated Around The Y 6 Line How Can I Find The Volume Of The Object Formed Quora



Consider The Parabola Y 4x X2 A Find The Slope Chegg Com




The Area Bounded By The Parabola Y 4x X 2 And X Axis Is Youtube



Consider The Parabola Y 4x X2 A Find The Slope Chegg Com
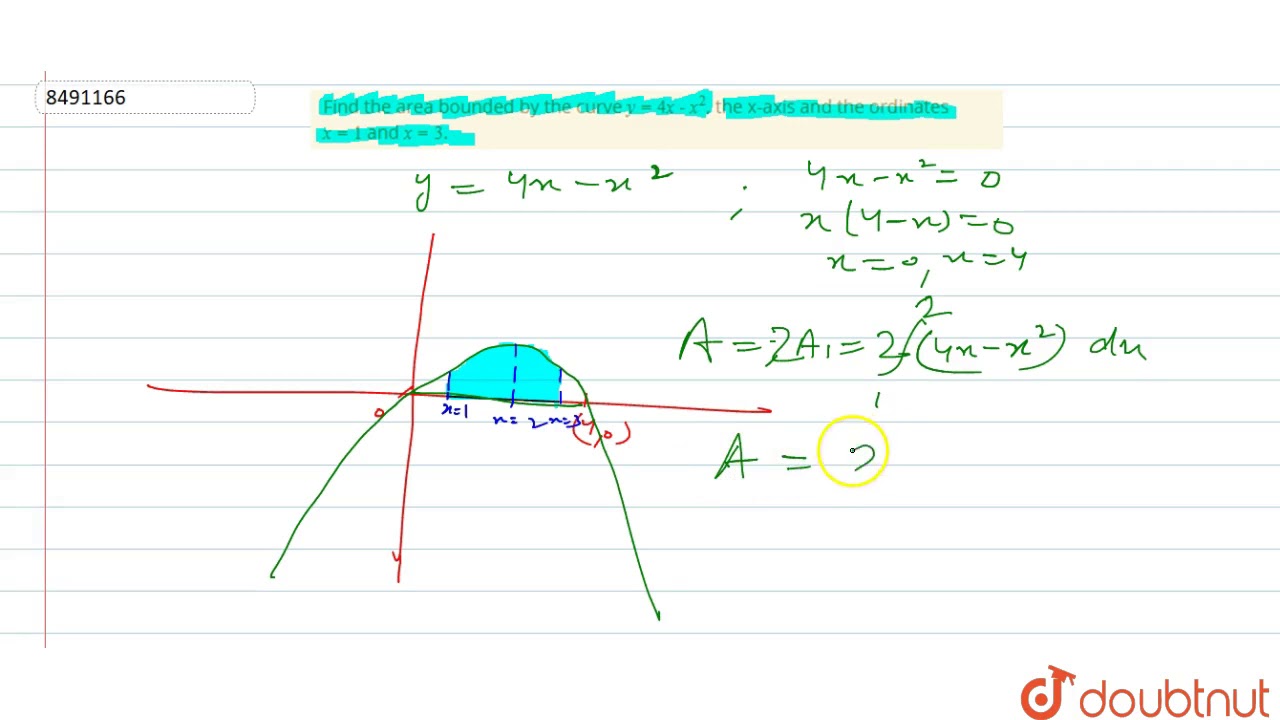



Find The Area Bounded By The Curve Y 4x X 2 The X Axis And The Ordinates X 1 And X 3 Youtube



The Region Between Y 4x X 2 And The X Axis Is Rotated Around The Y 6 Line How Can I Find The Volume Of The Object Formed Quora




What Is The Area Bounded By X Axis And The Curve Math Y 4x X 2 Math Quora



Exploration Of Parabolas




Solved Q3 A Find The Area Of The Region Of R As Shown I Chegg Com



Solution Graph The Parabola Y X2 4x 6
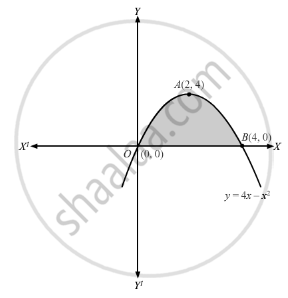



Find The Area Lying Above The X Axis And Under The Parabola Y 4x X2 Mathematics Shaalaa Com




2 Find The Area Lying Above The X Axis And Under Gauthmath




Answered Parabola Y 4x X At The Point 1 3 Bartleby




Graph The Parabola Y X 2 4x 1 Youtube




Sketch The Region R That Lies Below The Parabola Y 4x X 2 Above The X Axis And Above The Line Y 3x 6 Find The Area Of The Region R Study Com




The Area Bounded By The Parabola Y 4x X 2 And X Axis Is
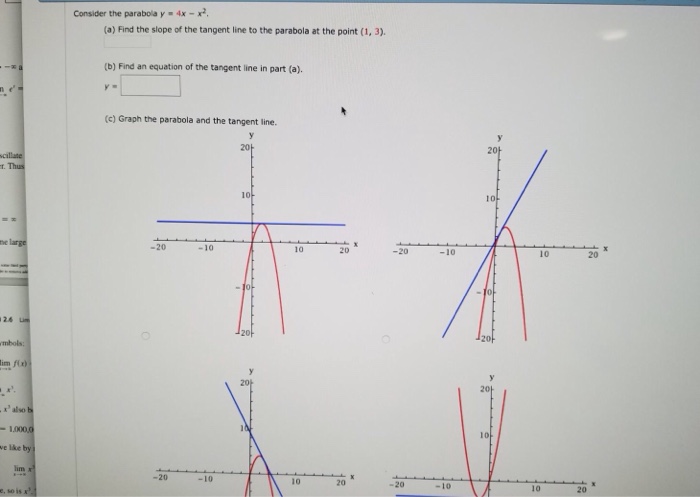



Consider The Parabola Y 4x X2 A Find The Slope Chegg Com




Graph Of Y 4x 2 Novocom Top
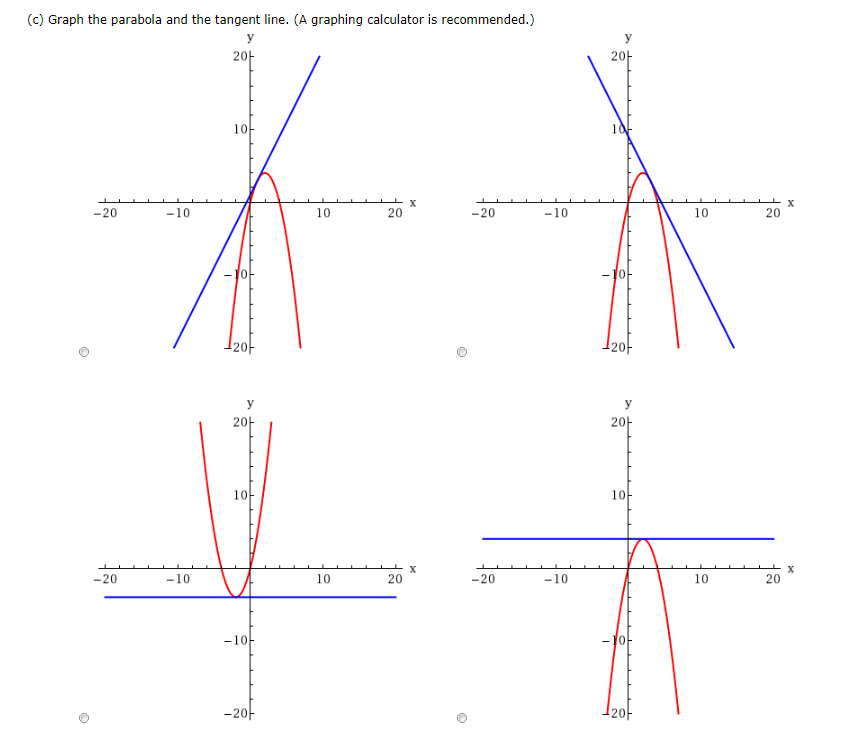



Consider The Parabola Y 4x X2 A Find The Slope M Chegg Com




In What Ratio Does The X Axis Divide The Area Of The Region Bounded By The Parabolas Y 4x X2 And Y X2 X Mathematics Shaalaa Com




Find The Area Of The Region Bounded By Y 2 4x X 1 X 4 And The



Consider The Parabola Y 4x X2 A Find The Slope Chegg Com




What Is The Area Bounded By X Axis And The Curve Math Y 4x X 2 Math Quora




Ex 21 1 Q4 Find The Area Lying Above The X Axis And Under The Parabola Y 4x X 2



How To Sketch A Parabola Example 2 Y X 2 4x 12 Youtube



Solved Consider The Parabola Y 4x X 2 A Find The S Chegg Com




Find The Area Bounded By The Parabola Y 6 4x X 2 And The Line Y 2x 2 Include A Sketch Of The Area Study Com




Write The Definite Integral That Represents The Area Of The Region Enclosed By The Parabola Y 4x X 2 And The X Axis Then Evaluate The Integral Study Com



In What Ratio Does The X Axis Divide The Area Of The Region Bounded By The Parabolas Y 4x X 2 And Y X 2 X Sarthaks Econnect Largest Online Education Community




The Area Bounded By The X Axis And The Curve Y 4x X 2 3 Is Youtube




Sketch The Region R That Lies Below The Parabola Y 4x X 2 Above The X Axis And Above The Line Y 3x 6 Find The Area Of This Region R Study Com




Compute The Volume Of The Solid Generated By Revolving About The X Axis The Region Bounded By The Line X 2y 0 And The Parabola Y 2 4x Study Com




Hitunglah Luas Dataran Yang Dibatasi Oleh Parabola Y 4x X Dan Sumbu X Brainly Co Id




Grafica De La Parabola Y 4x X2 Donde X Es 2 1 0 1 2 3 4 Brainly Lat



1




Graph Of Y 4x Novocom Top



How To Find The Volume Of The Solid Generated By Revolving The Region Bounded By Math Y 4x X 2 Math Math Y X Math About The Y Axis Quora




Find The Area Of The Region Bounded By The Parabola Y 2 4x The X Axis And The Lines X 1 And Youtube



Solution There Are Two Tangent Line To The Curve Y 4x X 2 That Pass Through The Point 2 5 Find The Equations Of These Two Lines And Make A Sketch To Verify Your Results




What Is The Area Of The Region Bounded By The Parabola Y 2 4x And The Line X 1 Quora



How To Graph Y 4x 2 Quora



Find The Area Bounded By Y 2lt 4x X 2 Y 2geq2x A N Dxlt Y 2 In




The Are Bounded By The Curve Y 4x X 2 And The X Axis Is



The Area Bounded By The Curves Y 2 4x And X 2 4y Youtube



Search Q Y 5e2 3d4x Tbm Isch



Find The Area Lying Above The X Axis And Under Gauthmath
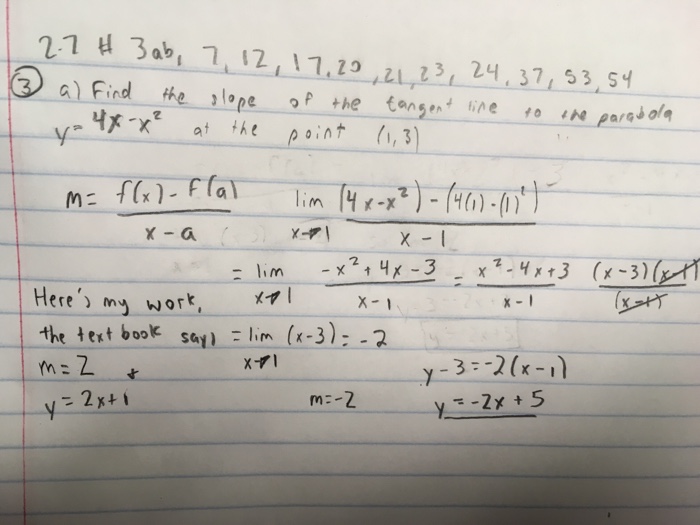



Find The Slope Of The Tangent Line To The Parabola Y Chegg Com




The Area Bounded By The X Axis And The Curve Y 4x X 2 3 Is




Answered 4x X2 Consider The Parabola Y A Bartleby



Find The Area Of The Region Bounded By The Parabola Y 2 4x The X Axis And The Lines X 1 And X 4 Sarthaks Econnect Largest Online Education Community




What Is The Volume Of The Region Bounded By Y 4x X 2 And Y X 2 If Rotated About The Line X 4 Quora



Ex 8 1 11 Find Area Bounded By Y2 4x And Line X 3



Solved Consider The Parabola Y 4x X2 A Find The Slope M Of The Tangent Line To The Parabola At The Point 1 3 I Using This Denition The Course Hero



2 Find The Area Lying Above The X Axis And Under Gauthmath
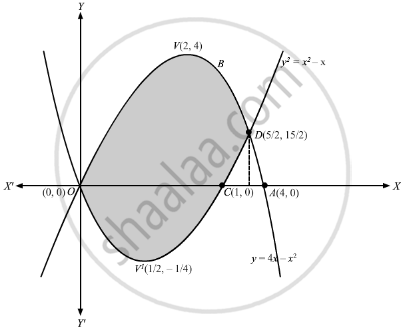



Find The Area Enclosed By The Parabolas Y 4x X2 And Y X2 X Mathematics Shaalaa Com




Answered Example 3 Find The Point On The Bartleby



Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube




The Area Bounded By The Parabola Y 4x 2 Y X 2 9 And The Li



Q Tbn And9gcqmzeprjzulnfzqoglblqubgspfyc0tx5w8skururanec4oa9 Usqp Cau




Find The Area Bounded By The Curve Y 4x X 2 The X Axis And The
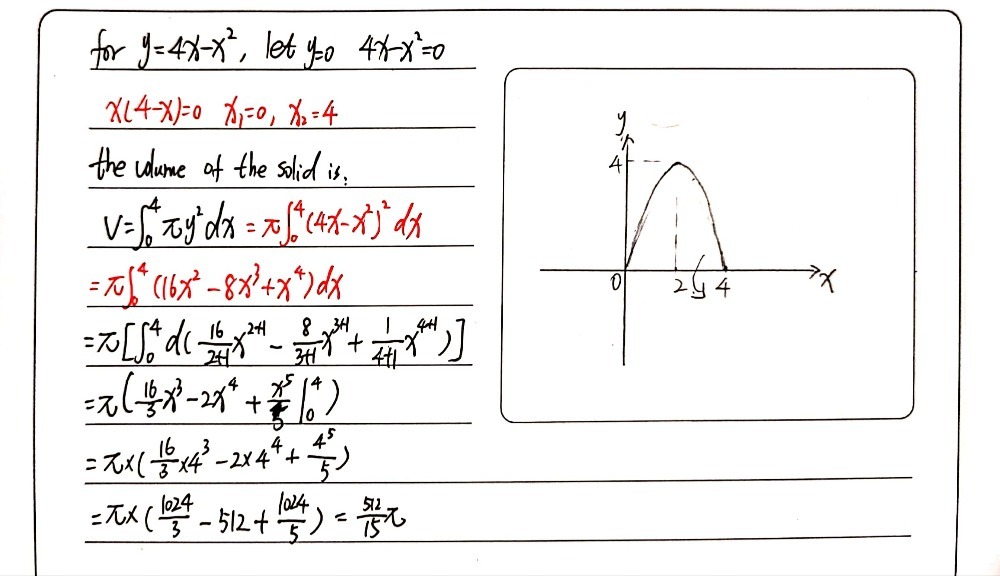



Q1 The Region Bounded By The Parabola Y 4x X2 And Gauthmath




Solution Find The Area In The First Quadrant Bounded By The Parabola Y 2 4x X 1 And X 3



What Is The Area Of The Curve Y 4x X X Axis And The Line X 0 X 6 Quora




Luas Daerah Yang Dibatasi Oleh Parabola Y 4x X 2 Y 2x 8 Dan Sumbu Y Brainly Co Id




Y X2 Double Integral Of The Area Of The Y 4x X Region Homeworklib



How To Graph A Parabola Y 4x 2 Socratic




Q1 The Region Bounded By The Parabola Y 4x X2 And Gauthmath



Example 14 Prove That Y2 4x X2 4y Divide Area Of Square



Scalcet8 2 7 003 2 5 Points Consider The Parabola Chegg Com



Solution When Does Y Kx Intersect The Parabola Y X 1 2 Quadratics Underground Mathematics



Find The Area Lying Above The X Axis And Under The Parabola Y 4x X 2 Sarthaks Econnect Largest Online Education Community



Q Tbn And9gcs Howml Gtefickaomlyurulemojqn R Wz C Wn92unyzdgby Usqp Cau
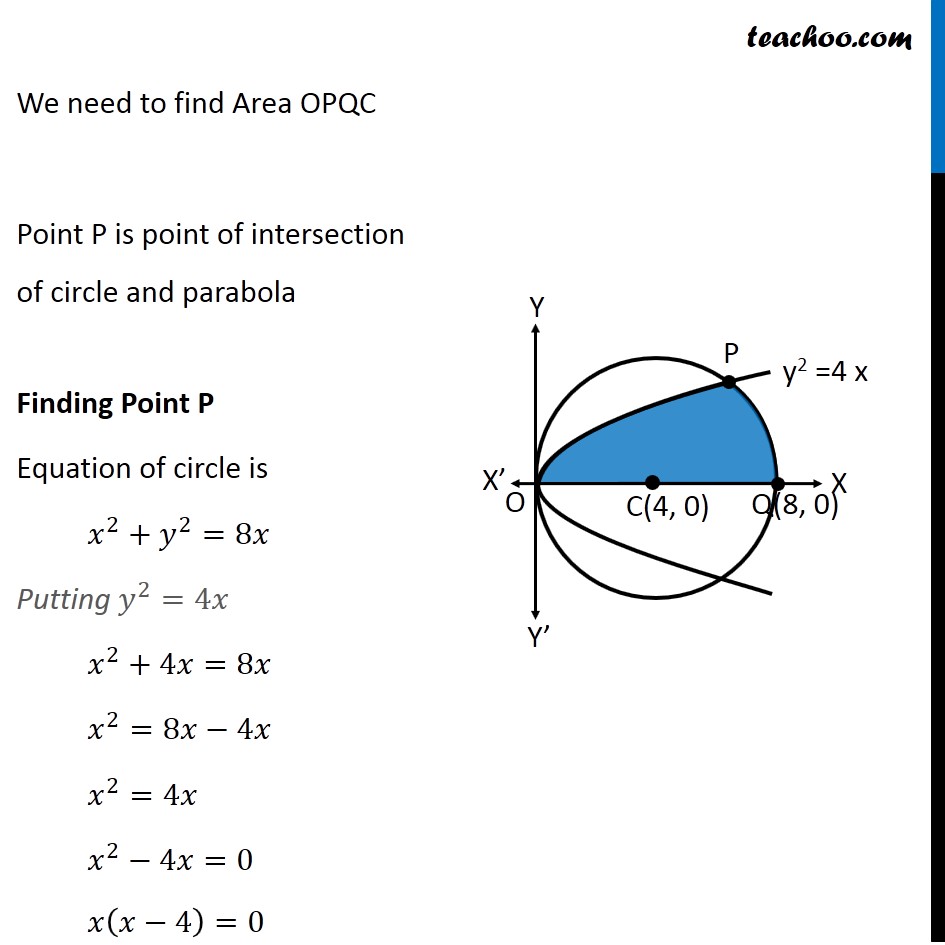



Example 7 Find Area Lying Above X Axis Included B W Circle



What Is The Area Bounded By The Curve Y 4x X And The Lines X 0 And Y 4 Quora




Y 4x X At The Point 1 3 0 Using Definition 1 I Chegg Com




Parabolas Ppt Download



0 件のコメント:
コメントを投稿